7784. Золотые слитки
Разбойники с большой дороги Джон и Боб ограбили караван и в качестве
добычи получили три золотых слитка. Решив поделить добычу по-братски, Джон и
Боб взвесили слитки и выяснили, что они весят x1, x2
и x3 фунтов,
соответственно.
Теперь Джон и Боб хотят поделить слитки так, чтобы каждому из них
досталось равное количество золота. Им не хотелось бы пилить слитки, но
деваться некуда. Обсудив ситуацию, они решили, что если смогут, поделят добычу
как есть, а если нет, то сумеют-таки распилить один слиток на две части.
Распилить два или все три слитка они уже не смогут.
Помогите Джону и Бобу выбрать, какой слиток распилить на две части, и на
какие части его следует распилить, чтобы после этого можно было поделить добычу
поровну.
Вход. Первая строка
входных данных содержит три целых числа: x1, x2 и x3 (1 ≤ xi
≤ 108, сумма весов слитков чётна).
Выход. Если
невозможно распилить один слиток таким образом, что после этого можно поделить
золото поровну, выведите -1.
Если Джон и Боб и так могут поделить золото поровну,
выведите 0.
В противном случае на первой строке выведите число 1,
если следует распилить первый слиток, 2, если следует распилить второй слиток,
либо 3, если следует распилить третий слиток. На второй строке выведите два
положительных целых числа: веса частей, на которые следует распилить слиток. В
сумме две части должны давать исходный вес слитка. Так как суммарный вес золота
чётен, слиток всегда требуется распиливать на части, имеющие целый вес. Если возможных
решений несколько, выведите любое.
|
Пример входа |
Пример выхода |
|
2 3 3 |
2 2 1 |
РЕШЕНИЕ
математика
Анализ алгоритма
Сначала
проверим, можно ли совершить раздел слитков без разрезания. Это так, если имеет
место одно из условий: x1 + x2 = x3, x2 + x3 = x1 или x1 + x3 = x2.
Сложим три
слитка вместе (порядок не имеет значения). Каждый из разбойников должен
получить mid = (x1 + x2
+ x3) / 2 золота. По условию задачи сумма весов слитков четная, следовательно mid целое.
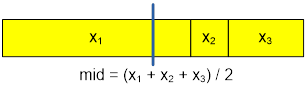
Разделить одним разрезом золото всегда возможно.
Остается определить кусок и на какие части его следует разделить.
·
Если mid < x1, то
делить следует первый кусок на части mid и x1 – mid.
·
Если x1 < mid < x1 + x2, то
делить следует второй кусок на части mid – x1 и x1 + x2 – mid.
·
Если x1 + x2 < mid, то
делить следует третий кусок на части mid – x1 – x2 и mid.
Реализация
алгоритма
Читаем входные данные. Вычисляем
количество золота mid, которое должны
получить каждый из разбойников.
scanf("%d %d %d",&a,&b,&c);
mid = (a +
b + c) / 2;
Проверяем, можно ли разделить золото
без разрезаний.
if (a + b == mid || a + c == mid || b + c == mid)
{
puts("0");
return 0;
}
Если надо резать первый кусок.
if (mid < a)
{
printf("1\n%d
%d\n",mid,a - mid);
return 0;
}
Если надо резать второй кусок.
if (mid < a + b)
{
printf("2\n%d
%d\n",mid - a,a + b - mid);
return 0;
}
Если надо резать третий кусок.
printf("3\n%d %d\n",mid - a - b,mid);